Pengertian dan Cara Uji Paired Sample T Test dengan SPSS

Pengertian Paired Sample T Test 

Paired Sample T Test adalah analisis dengan melibatkan dua pengukuran pada subjek yang sama terhadap suatu pengaruh atau perlakuan tertentu. Pengukuran pertama dilakukan sebelum diberi perlakuan tertentu dan pengukuran kedua setelah diberikan perlakuan. Tujuan dari uji paired sample t test ini untuk melihat apakah terdapat perbedaan rata-rata dari dua sampel yang saling berpasangan. Arti dari sampel berpasangan yaitu subjek yang diteliti sama dan adanya perlakuan dari subjek tersebut.

A. Syarat Uji Paired Sample T Test

Uji paired sample t test merupakan bagian dari analisis parametrik, sehingga data yang diperoleh harus berdistribusi normal. Tentunya untuk mengetahui apakah data yang diperoleh berdistribusi normal atau tidak maka perlu melakuan uji normalitas. Setelah melakukan uji normalitas ternyata diperoleh data tidak normal, maka alternatif yang dapat digunakan adalah dengan uji wilcoxon. Uji wilcoxon ini merupakan analisis statistik non parametrik.

B. Contoh Kasus Paired Sample T Test

Berikut ini kami berikan satu contoh kasus paired sample t test, yang nantinya di analisis menggunakan SPSS.

Suatu rumah sakit melakukan percobaan treatment diet khusus kepada para pasien yang menderita tekanan darah tinggi. Sebelum dilakukan secara masal, dilakukan tes percobaan dengan treatment diet khusus selama 3 bulan terhadap beberapa pasien. Sampel di ambil secara random. Sebelum treatment, dilakukan pengukuran tekanan darah, kemudian akan diukur kembali setelah treatment. Berikut ini hasil pengukuran tekanan darah sebelum dan sesudah diberikan treatment:

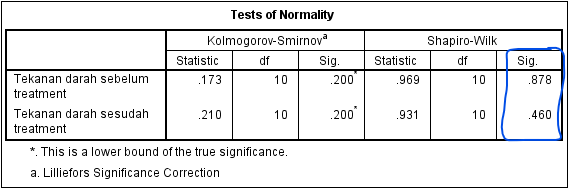
Sebelum kita melakukan analisis paired sample t test, maka terlebih dahulu kita harus mengetahui apakah data pengukuran tekanan darah telah berdistribusi normal atau tidak. Untuk mengetahui apakah data berdistribusi normal atau tidak, maka memerlukan uji normalitas. Berikut ini output uji normalitas dengan SPSS dapat dilihat pada gambar berikut ini:

Berdasarkan tabel Test of Normality pada bagian Shapiro-Wilk, diperoleh nilai Sig. untuk variabel Tekanan Darah Sebelum Treatment yaitu 0.878 dan variabel Tekanan Darah Sesudah Treatment yaitu 0.460. Karena kedua nilai tersebut lebih besar dari 0.05 maka dapat disimpulkan bahwa data sampel berdistribusi normal. Karena telah memenuhi asumsi dasar uji normalitas maka selanjutnya dapat melakukan uji paired sample t test.

Pembahasan lebih lengkap mengenai cara uji normalitas dapat Anda lihat melalui tautan berkut:

Baca Juga: Cara Uji Normalitas dengan SPSS

C. Langkah-langkah Uji Paired Sample T Test dengan SPSS

1. Buka software SPSS, kemudian klik Variable View untuk membuat variabel. Pada kolom Name ketik TK_Sebelum dan TK_Sesudah, lalu pada kolom Decimals ubah menjadi 1 (karena data terdapat 1 angka dibelakang koma). Pada kolom label ketik Tekanan Darah Sebelum Treatment dan Tekanan Darah Sesudah Treatment, lalu pada kolom Measure pilih Scale. Untuk kolom-kolom lainnya tidak perlu di setting (tidak perlu di ubah-ubah). Berikut ini tampilan Variable View.

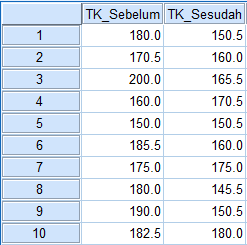
2. Selanjutnya kita input data dengan cara klik Data View, lalu menuliskan langsung data pada SPSS. Apabila data Anda sudah disusun di Microsoft Excel, maka bisa dengan cara copy dan paste.

3. Setelah selesai input data, selanjutnya ke analisis paired sampel t test dengan cara klik Analyze, pilih Compare Means, lalu pilih Paired-Sample T Test pada menu.

4. Setelah langkah tersebut, maka muncul kotak dialog Paired-Sample T-Test.

5. Klik variabel TK_Sebelum dan TK_Sesudah secara berurutan sehingga kedua variabel tersebut terblok. Kemudian klik tombol panah, sehingga pasangan variabel tersebut muncul pada kotak Paired Variables. 

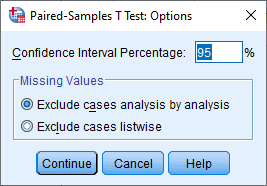
6. Selanjutnya klik Options, maka kotak dialog Paired-Sample T Test: Options muncul. Secara default, tingkat kepercayaan 95% (signifikansi 5%) dan Exclude cases analysis by analysis terpilih.

7. Klik Continue

8. Selanjutnya klik OK, sehingga output SPSS menampilkan hasil seperti berikut:

Tabel Paired Samples Statistics

Interpretasi Output Uji Paired Sample T Test dengan SPSS

Pada tabel Paired Sample Statistics, merupakan ringkasan hasil statistik deskriptif dari kedua sampel yang diteliti, yaitu Tekanan darah sebelum treatment dan tekanan darah setelah treatment. Rata-rata tekanan darah sebelum treatment yaitu 177.350, sedangkan rata-rata tekanan darah setelah treatment yaitu 160.800. Disini dapat dilihat bahwa secara diskriptif terdapat perbedaan rata-rata tekanan darah sebelum dan sesudah. Selanjutnya untuk membuktikan apakah perbedaan tersebut benar-benar signifikan atau tidak, maka kita perlu menafsirkan hasil uji paired sample t test pada tabel output Paired Samples Test.

Selanjutnya ada kolom N. N merupakan jumlah sampel yang digunakan, yaitu berjumlah 10. Standar Deviasi untuk variabel Tekanan Darah Sebelum Treatmen yaitu 14.4588, sedangkan Standar Deviasi untuk variabel Tekanan Darah Sesudah Treatment yaitu 11.7384. Std. Error Mean untuk variabel Tekanan Darah Sebelum Treatment yaitu 4.5723, sedangkan Std. Error Mean untuk variabel Tekanan Darah Sesudah Treatment yaitu 3.7120.

Tabel Paired Samples Correlations

Tabel output Paired Samples Correlations menunjukkan hasil korelasi atau hubungan antara kedua data tersebut. Pada tabel Paired Samples Correlations diperoleh nilai Sig. (signifikansi) 0.877. Karena nilai Sig. (0.877) >  α (0.05), maka tidak ada hubungan antara variabel Tekanan Darah Sebelum Treatment dengan Tekanan Darah Setelah Treatment.

Tabel Paired Samples Test

Tabel output Paired Samples Test, kolom Mean menunjukkan perbedaan rata-rata tekanan darah sebelum dan sesudah treatment yaitu sebesar 16.55. Kolom Std. Deviation menunjukkan standar deviasi dari nilai perbedaan rata-rata yaitu sebesar 18.1023. Kolom Std. Error Mean merupakan indeks variabilitas yaitu sebesar 5.7244. Kolom t merupakan hasil bagi antara nilai perbedaan rata-rata dengan standar error, diperoleh nilai t sebesar 2.891. Kolom df menunjukkan derajat kebebasan atau degree of freedom dengan nilai 9. Pada kolom Sig. (2-tailed) merupakan nilai probabilitas untuk mencapai t statistik, dimana nilai absolutnya adalah sama atau lebih besar dari t statistik. Diperoleh nilai Sig. (2-tailed) sebesar 0.018.

Pada tabel Paired Samples Test juga digunakan untuk menjawab hipotesis penelitian. Berikut ini hipotesis untuk kasus permasalahan di atas:

Hipotesis Contoh Kasus Uji Paired Sample T Test

H0 = Penurunan tekanan darah sebelum dengan sesudah treatment tidak signifikan.

H1 = Penurunan tekanan darah sebelum dengan sesudah treatment signifikan.

Pedoman Pengambilan Keputusan Uji Paired Sample T Test

Ada 2 cara dalam mengambil keputusan uji paired sample t test yaitu menggunakan perbandingan nilai t hitung dengan nilai t tabel dan menggunakan nilai Signifikansi. Berikut ini dasar pengambilan keputusannya.

Jika t hitung (nilai mutlak) < t tabel (α/2;n1-1) maka H0 diterima
Jika t hitung (nilai mutlak) > t tabel (α/2;n1-1) maka H0 ditolak

Atau

Jika nilai Sig. (signifikansi) > α (0.05) maka H0 diterima
Jika nilai Sig. (signifikansi) < α (0.05) maka H0 ditolak

Pedoman pengambilan keputusan dengan membandingkan nilai t hitung dengan t tabel

Pada tabel Paired Samples Test diperoleh nilai t hitung 2.891 > t tabel (0.025;9)  adalah 2.262 maka H0 ditolak. Karena H0 ditolak maka H1 diterima, jadi Penurunan tekanan darah sebelum dengan sesudah treatment signifikan.

Informasi Tambahan

Maksud dari t tabel (0.025;9) adalah df = 9. Angka 9 berasal dari jumlah sampel (10) dikurang 1. Permasalahan ini merupakan uji dua sisi, maka setiap sisinya memiliki nilai setengah α. Nilai α (alfa) adalah 0.05 maka setengah α adalah 0.025. Lalu mencari nilai t tabel  berdasarkan df 9 dan nilai α 0.025, sehingga diperoleh t tabel 2.262.

Baca juga: Cara Membuat Tabel T dengan SPSS dan Cara Mencari Nilai Tabel T 

Pedoman pengambilan keputusan dengan menggunakan nilai Signifikansi

Pada tabel Paired Samples Test diperoleh nilai Sig. (2-tailed) adalah 0.018 < 0.05  maka H0 ditolak. Karena H0 ditolak maka H1 diterima, jadi Penurunan tekanan darah sebelum dengan sesudah treatment signifikan.

Kesimpulan Contoh Kasus Uji Paired Sample T Test

Berdasarkan contoh kasus di atas yaitu tentang suatu rumah sakit yang melakukan percobaan treatment diet khusus kepada para pasien yang menderita tekanan darah tinggi. Setelah melakukan analisis menggunakan uji paired sample t test, diperoleh bahwa H1 diterima. Karena H1 diterima, maka Penurunan tekanan darah sebelum dengan sesudah treatment signifikan. Dengan kata lain, pemberian treatment untuk penderita tekanan darah tinggi berpengaruh terhadap penurunan tekanan darah. Berdasarkan hasil tersebut, maka pihak rumah sakit berhasil dalam melakukan percobaan treatment diet khusus kepada pasien penderita tekanan darah tinggi.

Anda juga dapat melihat tutorial Cara Uji Paired Sample T Test dengan SPSS dalam bentuk penjelasan video berikut ini:

Demikian artikel Pengertian dan Cara Uji Paired Sample T Test dengan SPSS, semoga artikel ini bermanfaat. Terimakasih telah mengunjunggi blog faqirilmu.com

Referensi:

Trihendradi, C., 2013. Step by Step IBM SPSS 21: Analisis Data Statistik. Yogyakarta: Penerbit Andi.
https://www.dqlab.id/analisis-data-dengan-mengenal-syarat-dan-contoh-paired-t-test#:~:text=Paired%20T%2DTest%20merupakan%20uji,yang%20saling%20berpasangan%20atau%20berhubungan.
http://www.spssindonesia.com/2016/08/cara-uji-paired-sample-t-test-dan.html